Laplace hàm truyền và sơ đồ khối

1. Giới Thiệu Về Laplace

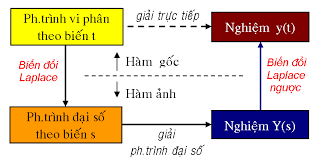
Laplace là một phương pháp quan trọng trong lĩnh vực toán học và kỹ thuật, được sử dụng để phân tích và mô hình hóa hệ thống động lực và hệ thống điều khiển. Đặc biệt, Laplace cho phép chuyển đổi các phương trình vi phân thường (dạng thời gian) sang miền tần số, từ đó giúp xác định phản ứng của hệ thống với các tín hiệu đầu vào khác nhau một cách hiệu quả.

2. Định Nghĩa Laplace Transform

Laplace Transform của một hàm $f(t)$ được định nghĩa bởi công thức sau:

F(s)=L{f(t)}=∫0∞e−stf(t) dtF(s) = \mathcal{L}\{f(t)\} = \int_0^\infty e^{-st} f(t) \, dtF(s)=L{f(t)}=∫0∞​e−stf(t)dt

Trong đó:

• $s$ là biến phức (được gọi là biến Laplace),
• $t$ là biến thời gian,
• $f(t)$ là hàm thời gian cần biến đổi,
• $F(s)$ là hàm tần số (transformed function) trong miền Laplace.

Điều này cho phép biểu diễn hàm $f(t)$ trong miền tần số $s$, thay vì trong miền thời gian $t$, giúp dễ dàng hơn trong việc phân tích và giải quyết các vấn đề phức tạp của hệ thống điều khiển và xử lý tín hiệu.

3. Ứng Dụng của Laplace Transform

Laplace Transform được áp dụng rộng rãi trong các lĩnh vực sau:

• Hệ thống điều khiển và tự động hóa: Dùng để phân tích và thiết kế hệ thống điều khiển phản hồi, từ việc thiết lập hàm truyền và phản ứng tần số đến tối ưu hóa và điều chỉnh hệ thống.
• Xử lý tín hiệu: Áp dụng trong xử lý tín hiệu số, nơi mà việc biến đổi tín hiệu từ miền thời gian sang miền tần số là cần thiết để xử lý và phân tích tín hiệu một cách hiệu quả.
• Kỹ thuật điện và điện tử: Được sử dụng để mô hình hóa và phân tích các mạch điện, vi điều khiển, hệ thống điện tử và viễn thông.

4. Laplace Transform và Hàm Truyền

Laplace Transform của hàm thời gian $f(t)$ cho ta hàm tần số $F(s)$. Trong hệ thống điều khiển, hàm truyền (transfer function) là một phần quan trọng, được xác định bởi mối liên hệ giữa đầu vào và đầu ra của hệ thống.

a. Hàm Truyền (Transfer Function)

Hàm truyền $G(s)$ của một hệ thống là tỉ lệ của biến đổi Laplace của đầu ra $Y(s)$ so với đầu vào $U(s)$, khi điều kiện ban đầu của hệ thống là không đổi:

G(s)=Y(s)U(s)G(s) = \frac{Y(s)}{U(s)}G(s)=U(s)Y(s)​

Hàm truyền mô tả khả năng phản ứng của hệ thống với các tín hiệu đầu vào khác nhau trong miền tần số. Nó cũng cho biết về độ ổn định, thời gian phản hồi và độ phù hợp của hệ thống.

b. Hệ Thống Tuyến Tính và Hàm Truyền

Để sử dụng Laplace Transform hiệu quả, hệ thống phải đáp ứng được các điều kiện tuyến tính và cân bằng. Điều này có nghĩa là hàm truyền $G(s)$ phải là một hàm tuyến tính của biến $s$. Hệ thống tuyến tính có thể được mô tả bởi các phương trình vi phân tuyến tính với các hệ số hằng.

5. Sơ Đồ Khối Trong Hệ Thống Điều Khiển

Sơ đồ khối là một công cụ quan trọng để biểu diễn và phân tích hệ thống điều khiển. Nó giúp biểu thị mối quan hệ giữa các thành phần của hệ thống và các tín hiệu chạy qua từng phần của hệ thống.

a. Các Phần Tử Cơ Bản Trong Sơ Đồ Khối

• Hộp chấm (Summing junction): Biểu thị các điểm tổng hợp hay các điểm chấm.
• Khối chức năng (Function block): Biểu thị các chức năng toán học như tích phân, vi phân, nhân, chia.
• Khối hàm truyền (Transfer function block): Biểu thị các hàm truyền của các hệ thống con.
• Khối tham số (Parameter block): Biểu thị các thông số hoặc hằng số.

b. Sơ Đồ Khối Đơn Giản Và Ví Dụ

Một ví dụ sơ đồ khối đơn giản cho hệ thống điều khiển có thể bao gồm các phần tử sau:

• Đầu vào U(s): Biểu thị tín hiệu điều khiển.
• Hàm truyền G(s): Biểu thị phản ứng của hệ thống.
• Đầu ra Y(s): Biểu thị tín hiệu đầu ra.

Sơ đồ khối giúp cho việc phân tích và thiết kế hệ thống điều khiển trở nên trực quan và dễ dàng hơn. Nó cho phép kỹ sư điều khiển xem xét và điều chỉnh các phần tử của hệ thống một cách có hệ thống và logic.

6. Ứng Dụng Thực Tế Của Laplace và Sơ Đồ Khối

• Thiết kế hệ thống điều khiển: Giúp xác định và thiết kế các hệ thống điều khiển phản hồi với độ chính xác cao và ổn định.
• Phân tích hệ thống: Cho phép phân tích tần số và phản hồi của hệ thống để đảm bảo hoạt động hiệu quả và ổn định.
• Mô phỏng và mô hình hóa: Dùng để mô hình hóa các hệ thống phức tạp và xác định cách điều khiển phù hợp.

Kết Luận

Laplace Transform và sơ đồ khối là những công cụ mạnh mẽ trong lý thuyết hệ thống điều khiển và xử lý tín hiệu. Việc hiểu và áp dụng chúng không chỉ cần thiết cho các kỹ sư điều khiển mà còn cho những ai quan tâm đến các hệ thống tự động hóa và điện tử. Bằng cách áp dụng Laplace Transform và biểu diễn qua sơ đồ khối, người sử dụng có thể dễ dàng phân tích và điều chỉnh hệ thống để đạt được các yêu cầu thiết kế và hoạt động một cách hiệu quả và ổn định.